Python中做时间序列分析

 1、 读入数据做时序图

# -*- coding: UTF-8 -*-     
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.tsa.stattools import adfuller as ADF
from statsmodels.graphics.tsaplots import plot_pacf
from statsmodels.stats.diagnostic import acorr_ljungbox
from statsmodels.tsa.arima_model import ARIMA
import numpy as np
from pandas import Series,DataFrame


data=pd.read_csv(r'C:/Users/Administrator/Desktop/stock_px.csv',sep=',',
	names=['date','APPL','MSFT','XOM','SPX'],skiprows=1,index_col='date')
data = pd.DataFrame(data,dtype=np.float64)
# print(data)
# 
# 时序图
plt.rcParams['axes.unicode_minus']=False
data.drop('SPX',1).plot()
plt.show()

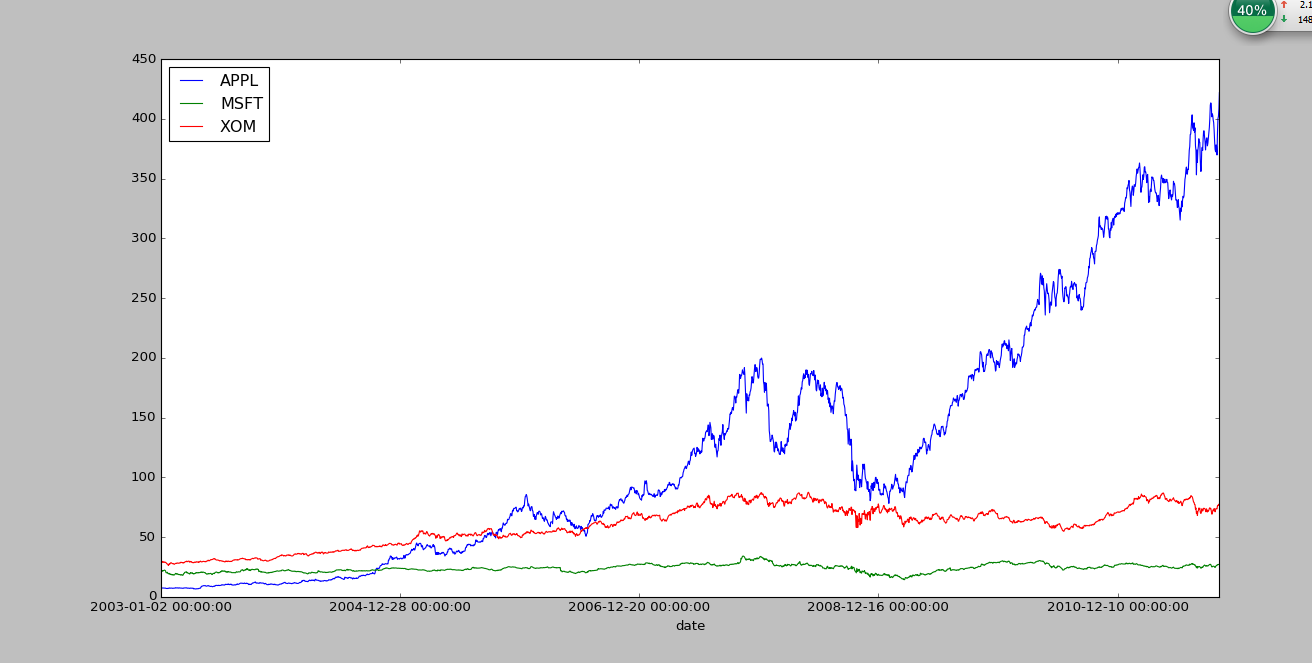
可以看到APPL的很不平稳，MSFT和XOM相对平稳些
2、 做自相关图

# 自相关图
plot_acf(data['APPL'])
plt.title(r'APPL-ACF')
plt.show()

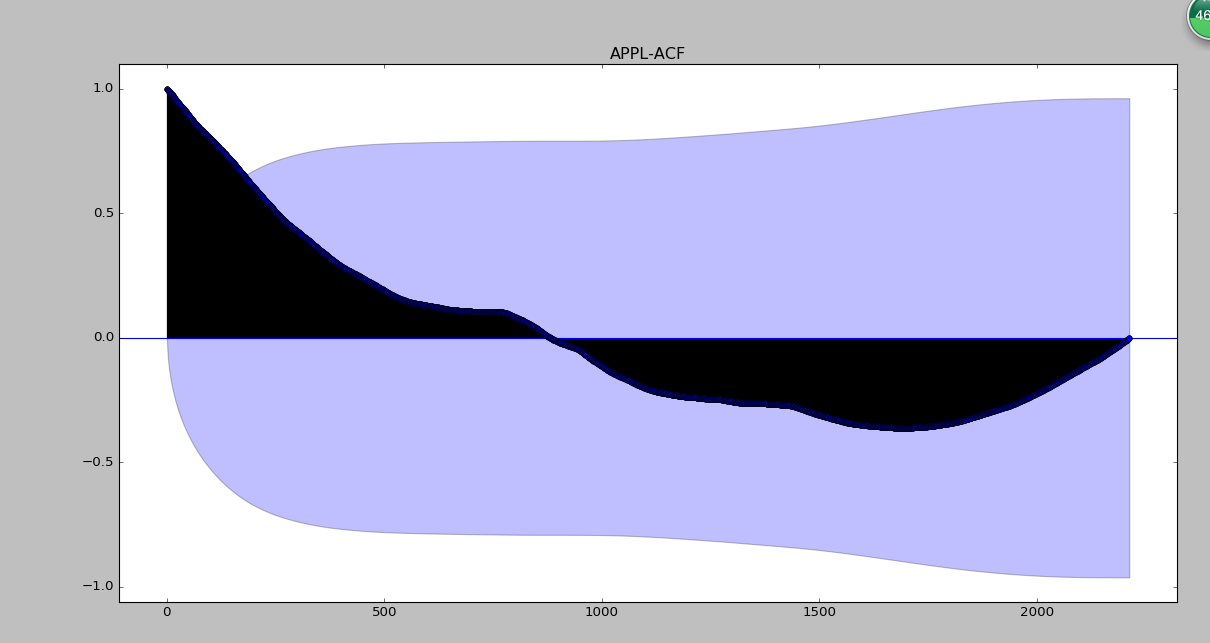
数量太多，不便于查看，下面只取出前100个

plot_acf(data['APPL'].iloc[:100])
plt.title(r'APPL-ACF')
plt.show()

plot_acf(data['MSFT'].iloc[:100])
plt.title(r'MSFT-ACF')
plt.show()

plot_acf(data['XOM'].iloc[:100])
plt.title(r'XOM-ACF')
plt.show()

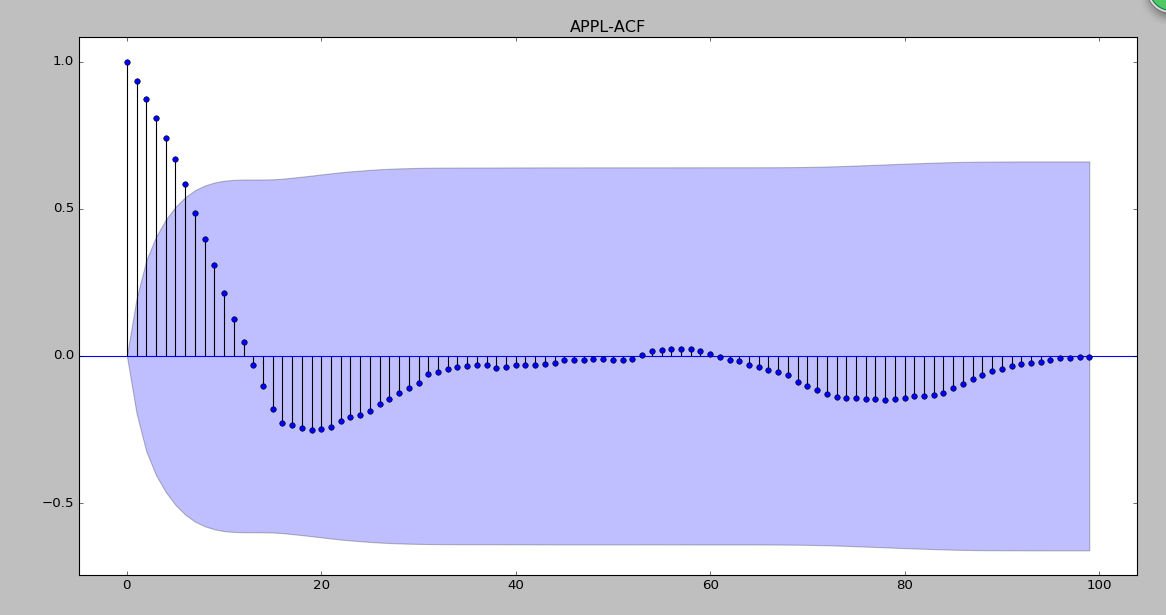
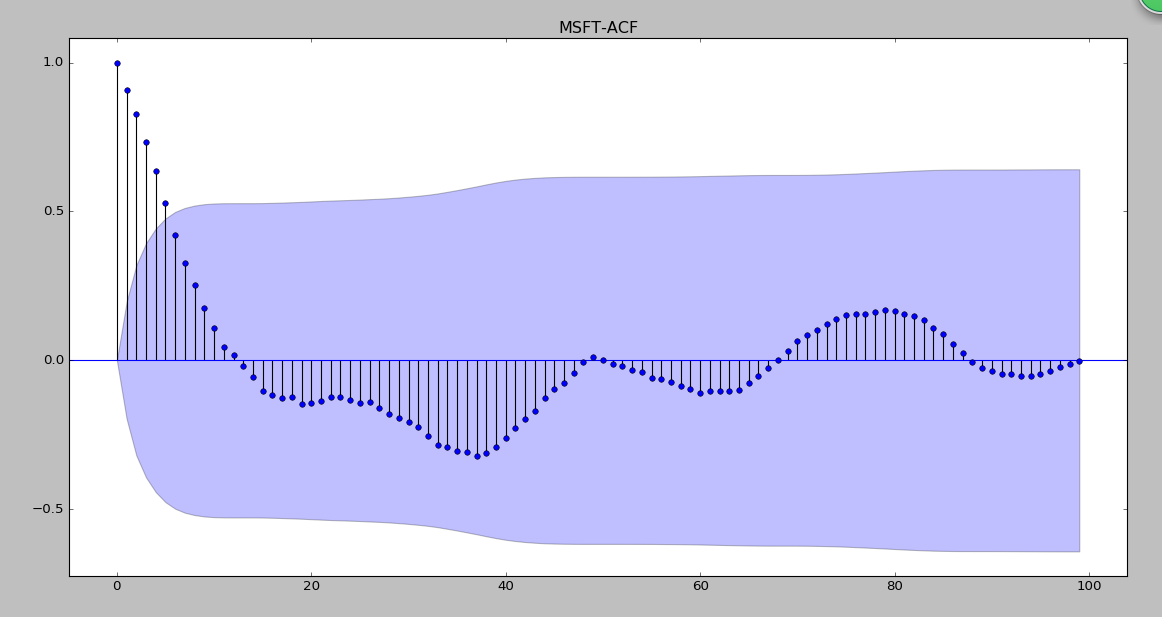
从跟上面可以知道APPL和XOM很不平稳，MFOT还相对平稳些
3、 下面做平稳性检验

#平稳性检测
print('APPL P-Value:',ADF(data['APPL'])[1])
print('MSFT P-Value:',ADF(data['MSFT'])[1])
print('XOM P-Value:',ADF(data['XOM'])[1])

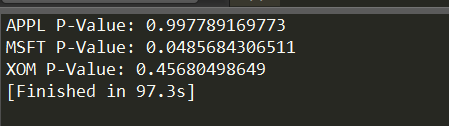
MSFT为平稳序列，但P-value带接近0.0.5，APPL和XOM为非平稳序列，对三者都做差分
4、 下面是一阶差分

#差分
data_diff=(data.drop('SPX',1)).diff().dropna()
data_diff.columns=['APPL-diff','MSFT-diff','XOM-diff']
data_diff.plot()
plt.title('diff-1')
plt.show()

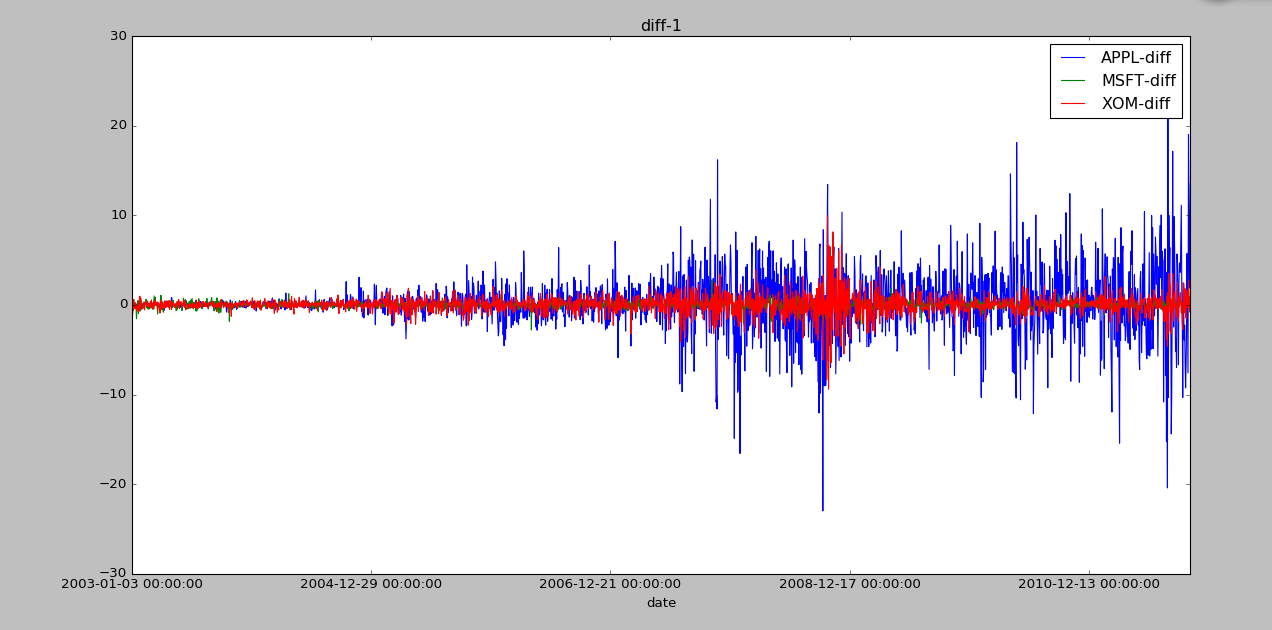
      各个股票的一阶差分自相关图

data_diff['APPL-diff'].plot()
plt.title('diff-1(APPL)')
plt.show()

data_diff['MSFT-diff'].plot()
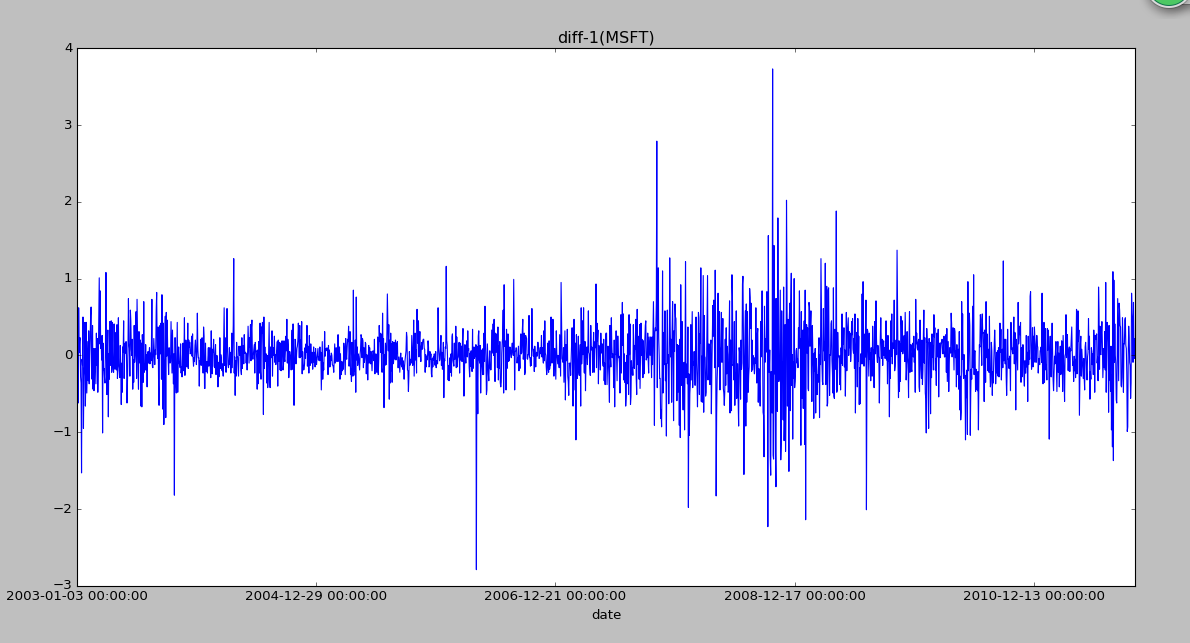
plt.title('diff-1(MSFT)')
plt.show()

data_diff['XOM-diff'].plot()
plt.title('diff-1(XOM)')
plt.show()

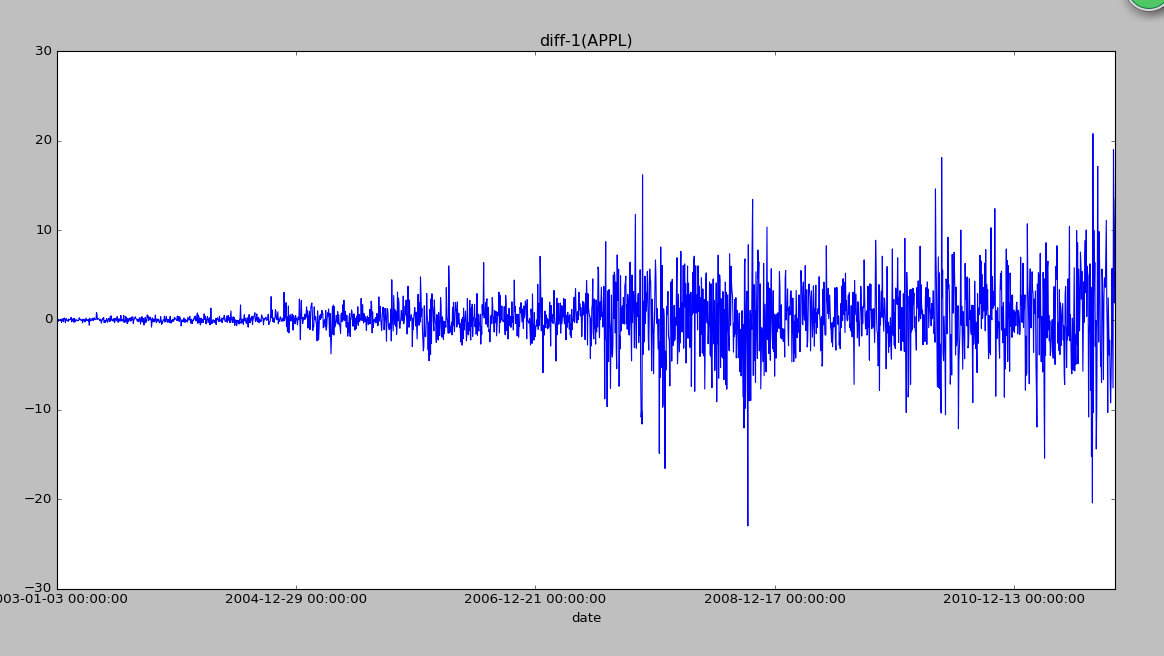
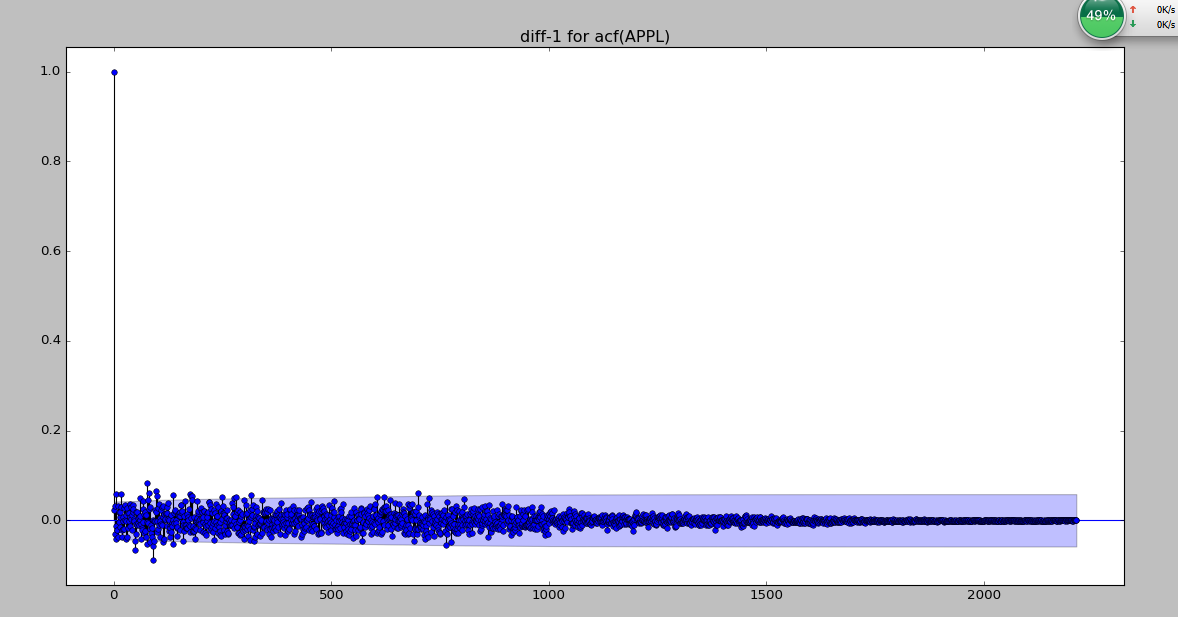
5、 一阶差分做检验

# # 自相关图
plot_acf(data_diff['APPL-diff'])
plt.title('diff-1 for acf(APPL)')
plt.show()

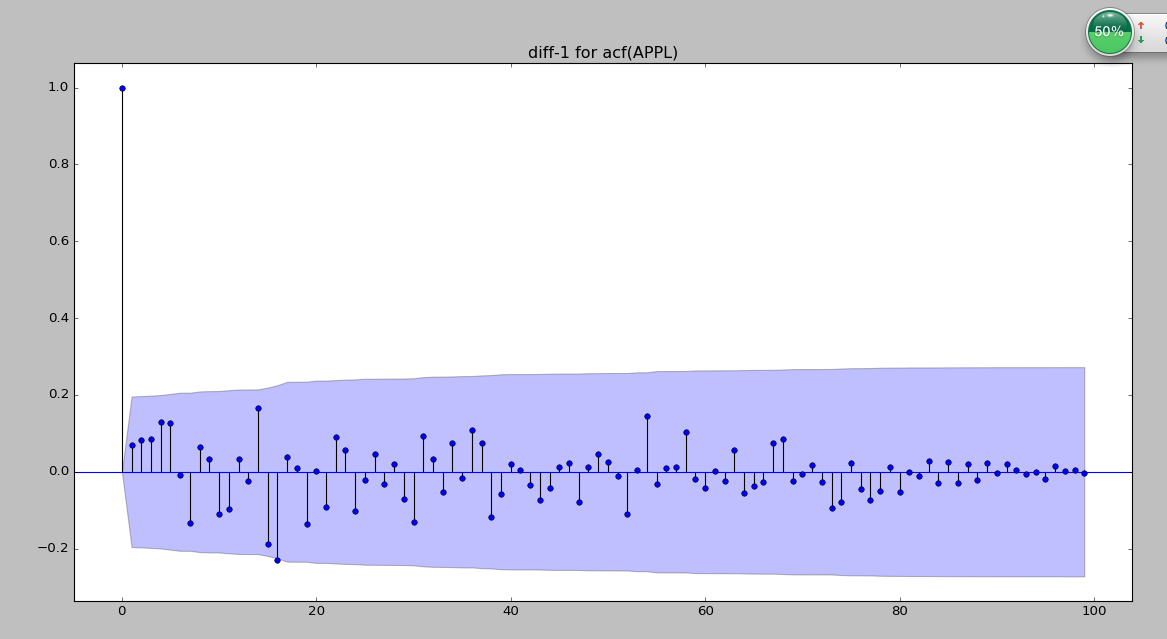
将其放大，值选取前100个

plot_acf(data_diff['APPL-diff'].iloc[:100])
plt.title('diff-1 for acf(APPL)')
plt.show()

plot_acf(data_diff['MSFT-diff'].iloc[:100])
plt.title('diff-1 for acf(MSFT)')
plt.show()

plot_acf(data_diff['XOM-diff'].iloc[:100])
plt.title('diff-1 for acf(XOM)')
plt.show()

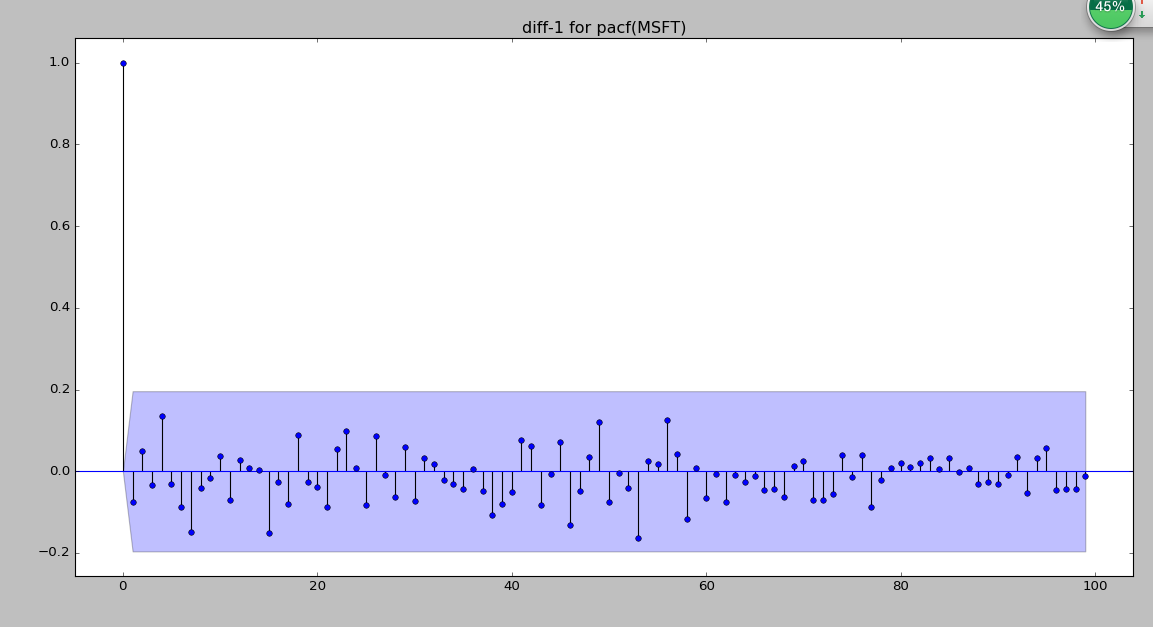
偏自相关图：

plot_pacf(data_diff['APPL-diff'].iloc[:100])
plt.title('diff-1 for pacf(APPL)')
plt.show()

plot_pacf(data_diff['MSFT-diff'].iloc[:100])
plt.title('diff-1 for pacf(MSFT)')
plt.show()

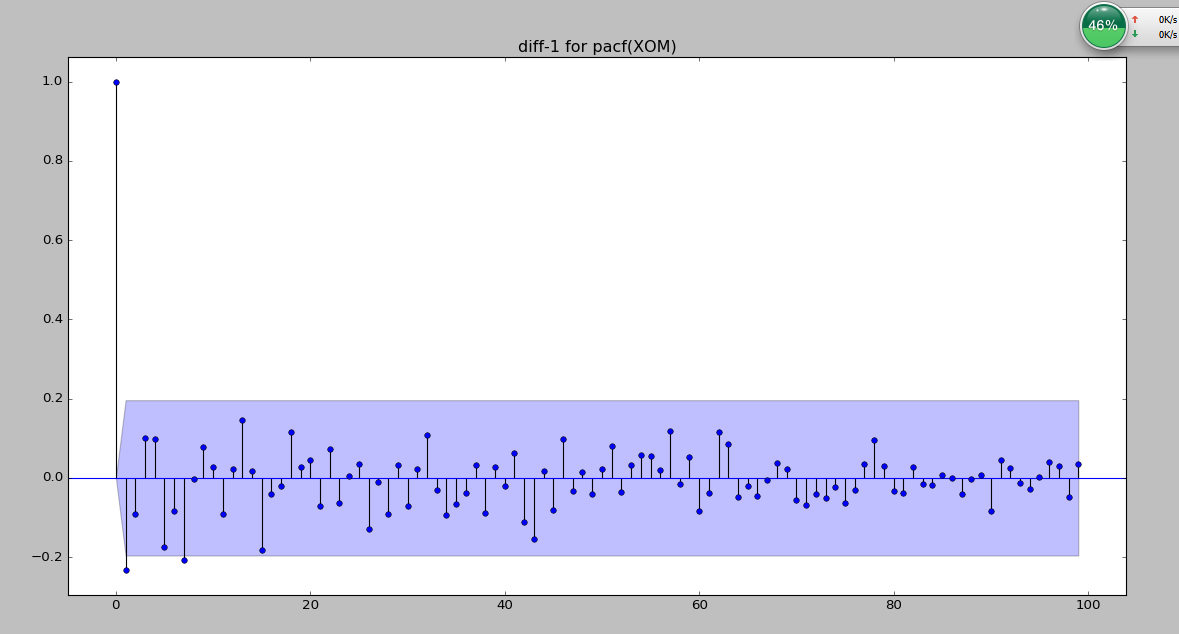
plot_pacf(data_diff['XOM-diff'].iloc[:100])
plt.title('diff-1 for pacf(XOM)')
plt.show()

平稳性检测

#平稳性检测
print('APPL P-Value:',ADF(data_diff['APPL-diff'])[1])
print('MSFT P-Value:',ADF(data_diff['MSFT-diff'])[1])
print('XOM P-Value:',ADF(data_diff['XOM-diff'])[1])

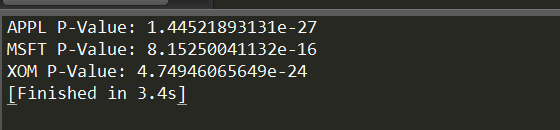
均远小于0.05，序列平稳
白噪声检验

# #白噪声检验 
print("APPL白噪声检验(P-value):",acorr_ljungbox(data_diff['APPL-diff'], lags=1)[1] )
print("MSFT白噪声检验(P-value):",acorr_ljungbox(data_diff['MSFT-diff'], lags=1)[1] )
print("XOM白噪声检验(P-value):",acorr_ljungbox(data_diff['XOM-diff'], lags=1)[1] )

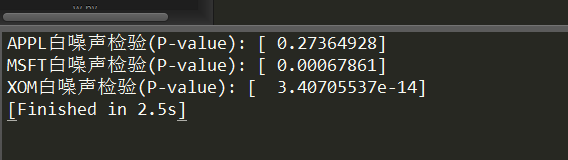
APPL的P值大于0.05，不排除白噪声，MSFT和XOM排除白噪声
6、 定阶

# AAPL建模
pmax=int(len(data_diff['APPL-diff'])/10)
qmax=int(len(data_diff['APPL-diff'])/10)
bic_matrix=[] 
for p in range(pmax+1):
    tmp=[]
    for q in range(qmax+1):
        try: 
            tmp.append(ARIMA(data['APPL'],(p,1,q)).fit().bic)
        except:
            tmp.append(1.1)
    bic_matrix.append(tmp)
bic_matrix=pd.DataFrame(bic_matrix) 
p,q=bic_matrix.stack().idxmin() 
print ('BIC最小的p值和q值为: %s、%s'%(p,q))
model=ARIMA(data['APPL'],(0,1,0)).fit()#建立ARIMA(0,1,0)模型
model.summary() 

# 
# MSFT建模
# pmax=5
# qmax=5
# bic_matrix=[] 
# for p in range(pmax+1):
#     tmp=[]
#     for q in range(qmax+1):
#         try: 
#             tmp.append(ARIMA(data['MSFT'],(p,1,q)).fit().bic)
#         except:
#             tmp.append(1)
#     bic_matrix.append(tmp)
# bic_matrix=pd.DataFrame(bic_matrix) 
# p,q=bic_matrix.stack().idxmin() 
# print (u'BIC最小的p值和q值为: %s、%s'%(p,q)) 
# model=ARIMA(data['MSFT'],(p,1,q)).fit() #建立ARIMA(0,1,1)模型
# model.summary() #给出一份模型报告




# pmax=int(len(data_diff['APPL-diff'])/10)
# qmax=int(len(data_diff['APPL-diff'])/10)
# bic_matrix=[]
# for p in range(pmax+1):
#   tmp = []
#   for q in range(qmax+1):
#     try: #存在部分报错，所以用try来跳过报错。
#       tmp.append(ARIMA(data['XOM'], (p,1,q)).fit().bic)
#     except:
#       tmp.append(None)
#   bic_matrix.append(tmp)

# bic_matrix = pd.DataFrame(bic_matrix)
# p,q=bic_matrix.stack().idxmin() #先用stack展平，然后用idxmin找出最小位置。
# print (u'BIC最小的p值和q值为: %s、%s'%(p,q)) #0,1
# model=ARIMA(data['XOM'],(p,1,q)).fit() #建立ARIMA(0,1,1)模型
# model.summary() #给出一份模型报告

                            ARIMA Model Results                              
===================================================
Dep. Variable:                 D.AAPL   No. Observations:                 2213
Model:                 ARIMA(0, 1, 0)   Log Likelihood               -5731.237
Method:                           css   S.D. of innovations              3.225
Date:                Sat, 24 Sep 2016   AIC                          11466.474
Time:                        13:12:28   BIC                          11477.878
Sample:                    01-03-2003   HQIC                         11470.640
                         - 10-14-2011                                         
===================================================
                 coef    std err          z      P>|z|      [95.0% Conf. Int.]
------------------------------------------------------------------------------
const          0.1873      0.069      2.733      0.006         0.053     0.322
===================================================

MSFT的ARIMA模型拟合报告：
                             ARIMA Model Results                              
===================================================
Dep. Variable:                 D.MSFT   No. Observations:                 2213
Model:                 ARIMA(0, 1, 1)   Log Likelihood               -1127.640
Method:                       css-mle   S.D. of innovations              0.403
Date:                Sat, 24 Sep 2016   AIC                           2261.280
Time:                        13:13:45   BIC                           2278.387
Sample:                    01-03-2003   HQIC                          2267.529
                         - 10-14-2011                                         
===================================================
                   coef    std err          z      P>|z|      [95.0% Conf. Int.]
--------------------------------------------------------------------------------
const            0.0028      0.008      0.351      0.726        -0.013     0.018
ma.L1.D.MSFT    -0.0752      0.021     -3.498      0.000        -0.117    -0.033
                                    Roots                                    
===================================================
                 Real           Imaginary           Modulus         Frequency
-----------------------------------------------------------------------------
MA.1           13.3040           +0.0000j           13.3040            0.0000
-----------------------------------------------------------------------------

XOM的ARIMA模型拟合报告：

                             ARIMA Model Results                              
===================================================
Dep. Variable:                  D.XOM   No. Observations:                 2213
Model:                 ARIMA(2, 1, 3)   Log Likelihood               -3267.532
Method:                       css-mle   S.D. of innovations              1.059
Date:                Sat, 24 Sep 2016   AIC                           6549.063
Time:                        13:14:26   BIC                           6588.978
Sample:                    01-03-2003   HQIC                          6563.644
                         - 10-14-2011                                         
===================================================
                  coef    std err          z      P>|z|      [95.0% Conf. Int.]
-------------------------------------------------------------------------------
const           0.0219      0.017      1.284      0.199        -0.012     0.055
ar.L1.D.XOM    -1.4970      0.090    -16.722      0.000        -1.672    -1.322
ar.L2.D.XOM    -0.5351      0.085     -6.287      0.000        -0.702    -0.368
ma.L1.D.XOM     1.3333      0.087     15.238      0.000         1.162     1.505
ma.L2.D.XOM     0.1787      0.081      2.201      0.028         0.020     0.338
ma.L3.D.XOM    -0.2140      0.021    -10.334      0.000        -0.255    -0.173
                                    Roots                                    
===================================================
                 Real           Imaginary           Modulus         Frequency
-----------------------------------------------------------------------------
AR.1           -1.1026           +0.0000j            1.1026            0.5000
AR.2           -1.6948           +0.0000j            1.6948            0.5000
MA.1           -1.1927           -0.1691j            1.2046           -0.4776
MA.2           -1.1927           +0.1691j            1.2046            0.4776
MA.3            3.2206           -0.0000j            3.2206           -0.0000
-----------------------------------------------------------------------------

源码：

# -*- coding: UTF-8 -*-     
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.tsa.stattools import adfuller as ADF
from statsmodels.graphics.tsaplots import plot_pacf
from statsmodels.stats.diagnostic import acorr_ljungbox
from statsmodels.tsa.arima_model import ARIMA
import numpy as np
from pandas import Series,DataFrame


data=pd.read_csv(r'C:/Users/Administrator/Desktop/stock_px.csv',sep=',',
	names=['date','APPL','MSFT','XOM','SPX'],skiprows=1,index_col='date')
data = pd.DataFrame(data,dtype=np.float64)
# print(data)
# 
# 时序图
plt.rcParams['axes.unicode_minus']=False
data.drop('SPX',1).plot()
plt.show()

# 自相关图
plot_acf(data['APPL'])
plt.title(r'APPL-ACF')
plt.show()
plot_acf(data['APPL'].iloc[:100])
plt.title(r'APPL-ACF')
plt.show()

plot_acf(data['MSFT'])
plt.title(r'MSFT-ACF')
plt.show()
plot_acf(data['MSFT'].iloc[:100])
plt.title(r'MSFT-ACF')
plt.show()

plot_acf(data['XOM'])
plt.title(r'XOM-ACF')
plt.show()
plot_acf(data['XOM'].iloc[:100])
plt.title(r'XOM-ACF')
plt.show()

#平稳性检测
print('APPL P-Value:',ADF(data['APPL'])[1])
print('MSFT P-Value:',ADF(data['MSFT'])[1])
print('XOM P-Value:',ADF(data['XOM'])[1])

#差分
data_diff=(data.drop('SPX',1)).diff().dropna()
data_diff.columns=['APPL-diff','MSFT-diff','XOM-diff']
data_diff.plot()
plt.title('diff-1')
plt.show()

data_diff['APPL-diff'].plot()
plt.title('diff-1(APPL)')
plt.show()

data_diff['MSFT-diff'].plot()
plt.title('diff-1(MSFT)')
plt.show()

data_diff['XOM-diff'].plot()
plt.title('diff-1(XOM)')
plt.show()

# 
# 一阶差分检验
# # 自相关图
plot_acf(data_diff['APPL-diff'])
plt.title('diff-1 for acf(APPL)')
plt.show()

plot_acf(data_diff['APPL-diff'].iloc[:100])
plt.title('diff-1 for acf(APPL)')
plt.show()

plot_acf(data_diff['MSFT-diff'].iloc[:100])
plt.title('diff-1 for acf(MSFT)')
plt.show()

plot_acf(data_diff['XOM-diff'].iloc[:100])
plt.title('diff-1 for acf(XOM)')
plt.show()

# # 偏自相关图
plot_pacf(data_diff['APPL-diff'])
plt.title('diff-1 for pacf(APPL)')
plt.show()

plot_pacf(data_diff['APPL-diff'].iloc[:100])
plt.title('diff-1 for pacf(APPL)')
plt.show()

plot_pacf(data_diff['MSFT-diff'].iloc[:100])
plt.title('diff-1 for pacf(MSFT)')
plt.show()

plot_pacf(data_diff['XOM-diff'].iloc[:100])
plt.title('diff-1 for pacf(XOM)')
plt.show()
# 
# 
#平稳性检测
print('APPL P-Value:',ADF(data_diff['APPL-diff'])[1])
print('MSFT P-Value:',ADF(data_diff['MSFT-diff'])[1])
print('XOM P-Value:',ADF(data_diff['XOM-diff'])[1])

# #白噪声检验 
print("APPL白噪声检验(P-value):",acorr_ljungbox(data_diff['APPL-diff'], lags=1)[1] )
print("MSFT白噪声检验(P-value):",acorr_ljungbox(data_diff['MSFT-diff'], lags=1)[1] )
print("XOM白噪声检验(P-value):",acorr_ljungbox(data_diff['XOM-diff'], lags=1)[1] )



# AAPL建模
pmax=int(len(data_diff['APPL-diff'])/10)
qmax=int(len(data_diff['APPL-diff'])/10)
bic_matrix=[] 
for p in range(pmax+1):
    tmp=[]
    for q in range(qmax+1):
        try: 
            tmp.append(ARIMA(data['APPL'],(p,1,q)).fit().bic)
        except:
            tmp.append(1.1)
    bic_matrix.append(tmp)
bic_matrix=pd.DataFrame(bic_matrix) 
p,q=bic_matrix.stack().idxmin() 
print ('BIC最小的p值和q值为: %s、%s'%(p,q))
model=ARIMA(data['APPL'],(0,1,0)).fit()#建立ARIMA(0,1,0)模型
model.summary() 

# 
# MSFT建模
# pmax=5
# qmax=5
# bic_matrix=[] 
# for p in range(pmax+1):
#     tmp=[]
#     for q in range(qmax+1):
#         try: 
#             tmp.append(ARIMA(data['MSFT'],(p,1,q)).fit().bic)
#         except:
#             tmp.append(1)
#     bic_matrix.append(tmp)
# bic_matrix=pd.DataFrame(bic_matrix) 
# p,q=bic_matrix.stack().idxmin() 
# print (u'BIC最小的p值和q值为: %s、%s'%(p,q)) 
# model=ARIMA(data['MSFT'],(p,1,q)).fit() #建立ARIMA(0,1,1)模型
# model.summary() #给出一份模型报告




# pmax=int(len(data_diff['APPL-diff'])/10)
# qmax=int(len(data_diff['APPL-diff'])/10)
# bic_matrix=[]
# for p in range(pmax+1):
#   tmp = []
#   for q in range(qmax+1):
#     try: #存在部分报错，所以用try来跳过报错。
#       tmp.append(ARIMA(data['XOM'], (p,1,q)).fit().bic)
#     except:
#       tmp.append(None)
#   bic_matrix.append(tmp)

# bic_matrix = pd.DataFrame(bic_matrix)
# p,q=bic_matrix.stack().idxmin() #先用stack展平，然后用idxmin找出最小位置。
# print (u'BIC最小的p值和q值为: %s、%s'%(p,q)) #0,1
# model=ARIMA(data['XOM'],(p,1,q)).fit() #建立ARIMA(0,1,1)模型
# model.summary() #给出一份模型报告